直方图可以用来什么(直方图有什么作用)
简单总结如下, 详见后文:
直方图定义
维基百科上给出的定义是:
在统计学中,直方图(Histogram)是一种对数据分布情况的图形表示, 是一种二维, 它的两个坐标分别是统计样本和该样本对应的某个属性的度量, 以长条图(bar)的形式具体表现. 因为直方图的长度及宽度很适合用来表现数量上的变化, 所以较容易解读差异小的数值.
百度上给出的定义是:
直方图又称质量分布图, 是一种统计报告图, 由一系列高度不等的纵向条纹或线段表示数据分布的情况. 一般用横轴表示数据类型, 纵轴表示分布情况. 直方图是数值数据分布的精确图形表示, 这是一个连续变量(定量变量)的概率分布的估计, 并且被卡尔·皮尔逊(Karl Pearson)首先引入. 它是一种条形图. 为了构建直方图, 第一步是将值的范围分段, 即将整个值的范围分成一系列间隔, 然后计算每个间隔中有多少值. 这些值通常被指定为连续的, 不重叠的变量间隔. 间隔必须相邻, 并且通常是(但不是必须的)相等的大小.
总结一下直方图特征为: 二维图表, 横轴为数据(具有一定的连续性), 纵轴为数据分布(数据数量).
直方图作用
由于直方图的特性, 有很多的应用: 如在数据处理方面可以用来排序, 如在图像处理方面可以用来图像增强和图像分割.
直方图应用之排序
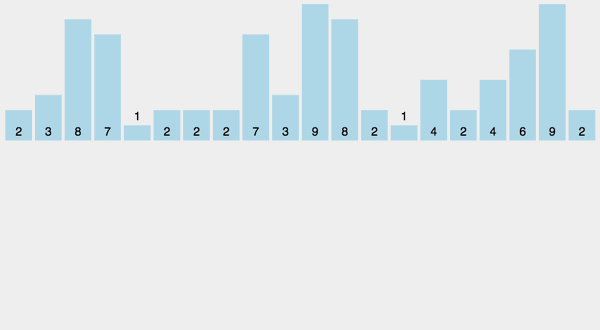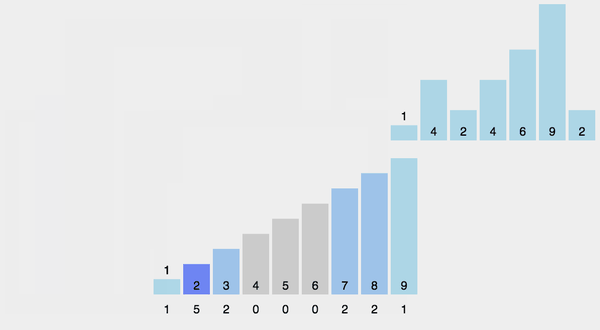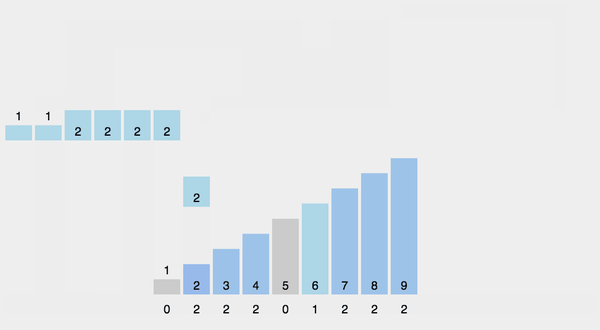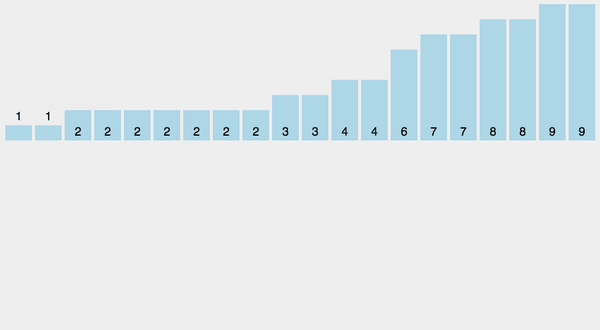
排序算法中有一大类使用的是非比较排序, 如下图所示为计数排序, 从图中可以看到, 排序过程中使用了直方图来统计数据, 由于直方图的横坐标有一定的连续性, 当数据统计完成, 也就完成排序的目的. 详细可以参见: 十大经典排序算法(动图演示) - 一像素 - 博客园 (cnblogs.com)
还有一些扩展应用, 如快速查找数据中的topN, 如用来加速中值滤波(快速查找中间数据)等.
直方图应用之图像增强
常见的使用直方图进行增强的方法就是直方图均衡(HE, Histogram Equalization), 对比度受限自适应直方图均衡(CLAHE, Contrast Limited Adaptive Histogram Equalization).
均衡的作用就是让直方图的分布更加均匀, 直方图分布越均匀, 其熵越大, 熵越大图像中包含的信息也就越多, 图像对比度就越高, 从而实现图像增强的效果. 如下图所示为HE的效果:
直方图应用之图像分割
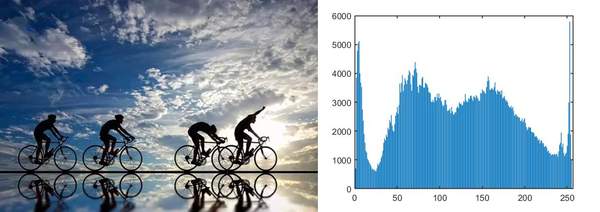
直方图是数据分布的直观表示, 直方图中的每一个波峰就代表一个目标的分布, 可以通过查看直方图中的波峰来确定图像中目标的个数及分布, 因而也可以用来对图像进行分割, 将直方图中的波峰进行划分即可以完成图像分割. 如下图所示为图像及其对应的直方图, 图中直方图有4个波峰(最右边2个波峰比较靠近, 认为是一个目标), 也可以看到图像上基本也有4个目标: 人影, 蓝天, 白云, 太阳.
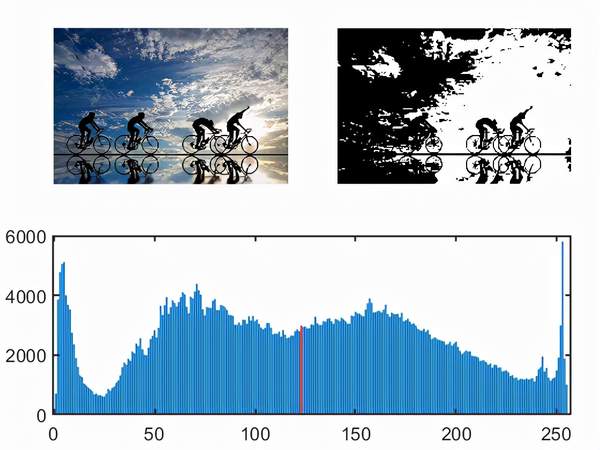
最常见的使用直方图进行图像分割的方法是大津阈值法(otsu), 如下所示为otsu实现效果:
otsu方法将直方图分为2个部分, 如上图所示红色线为分割阈值, 对于有多个目标的图像, 效果不是很好.
对于多目标图像分割, 可以使用迭代otsu, 进行多次分割, 也可以对直方图进行高斯拟合(假设目标分布服从高斯分布), 如下所示为高斯拟合进行分割结果: