用origin软件处理实验数据（origin数据处理） / 木子杰软件教程

1. 数据点的横坐标不是等间距时的曲线绘制

用实验数据作图时，会遇到数据点的横坐标不是等间距的情况，比如：

X：1，3，4，8，9，12，...

Y：10.2，10.5，11.4，11.8，10.9，10.2，...

如果只有一组实验数据，则按照普通的方法在Worksheet中分别输入X，Y的值，然后用“线符号”的方式绘图即可。

但是，当有多组此种情况的数据需要绘制在一个图中时，例如：

X1：1，3，4，8，9，12，...

Y1：10.2，10.5，11.4，11.8，10.9，10.2，...

X2：2，5，9，10，11，13，...

Y2：13.2，13.5，14.4，13.8，13.9，13.2，...

这时如果将两组数据的X值放在一列里，则Y1和Y2会出现不连续的情况，绘出的曲线发生间断。

解决的办法是：

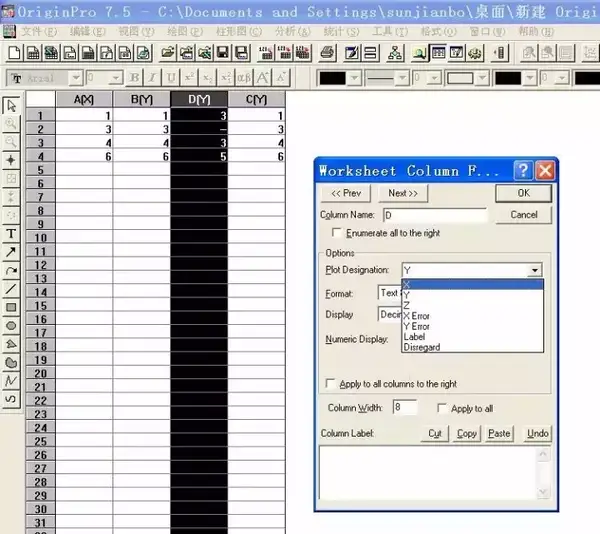
每组数据的X值都放在各自的X列中，绘出的每条曲线就都是连续的了。具体的操作如图1所示。

图1 改变数据列的坐标轴属性

2. 多图层下的绘图——图层的使用

1）两组数据的横坐标相差小，纵坐标相差大的情况

2）横坐标相差大，纵坐标相差小的情况

3）横坐标和纵坐标相差都大

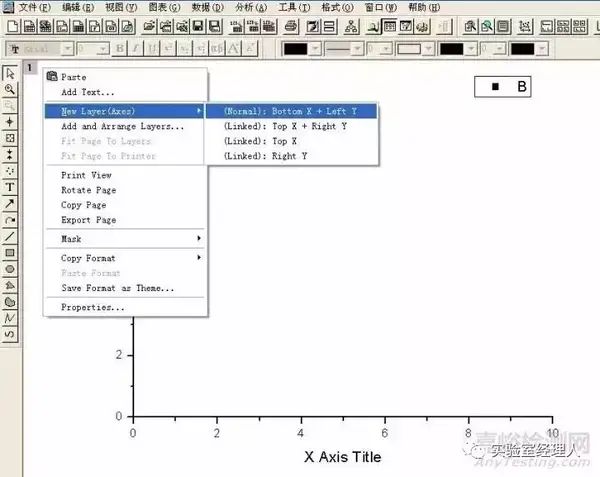
图层的建立如图2所示

图2 新图层的建立过程

3. 移动坐标轴及在一个图中出现多个坐标轴

增加两个新图层的方法设置三个纵坐标，在想要移动的y坐标轴上点右键打开坐标轴对话框，然后选“title&format---axis”下拉框选“at position=”然后在下面的框里输入想要移动多远就可以了。

4. 如何输入σ，±这样的符号

添加文本，然后点击Ctrl M，选择你所需的字符，插入就行了。

5. Origin中中文间距不一的问题

升级到7.5以上版本，问题解决

6. 添加误差棒

（1）计算标准偏差，将所有数据输入Excel, 分别计算每组数据的平均值

（2）将所有数据输入Excel，用公式“stdev”计算每组数据的标准偏差

（3）将X轴数据，平均值，标准偏差输入origin，然后选中标准偏差所在列--colomn--setas Y error , 然后选中所有数据
--plot--specialline/symbol--Y error

注：在Origin中计算平均值和标准差的方法，右键单击选中需要统计的数据列，在弹出菜单中选择“statistics on column(s)/row(s)”即可得到平均值（Mean）和标准差（Sd）

7. 设置数据列的值

（1）用系统自带函数设置

单击鼠标右键选中需要设置新值的数据列，从弹出菜单中选择“set column values...”命令，在弹出的对话框中设置需要用到的函数和数据列（选择了函数和列后别忘了单击后面的add function 和add column），最后单击OK，新计算出的数据出现在先前选中的数据列中。

（2）怎么求非自然数为底的幂函数

Origin中的自然数的幂函数ex很容易，用EXP函数就可以了，但是其它幂函数没有，例如：将一列数据转变为以10为底，数列为幂指数，用10^col(A)就可以了。（^ [kArit]求幂指数符号）

8. 绘制函数

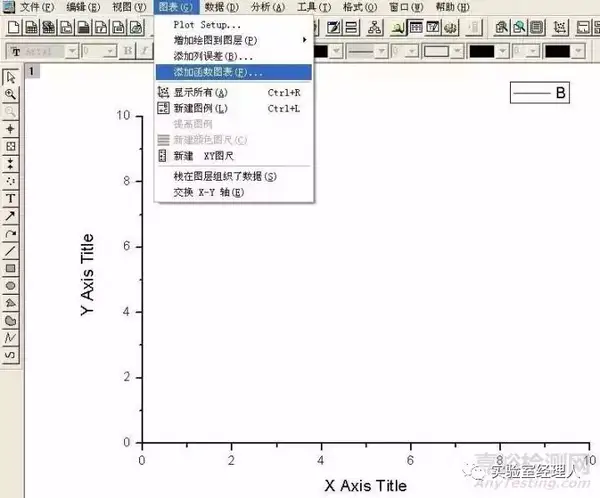
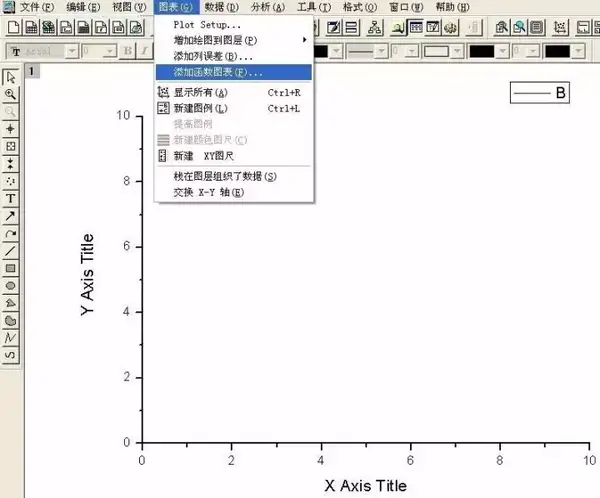
有的时候，我们有一个函数，想绘制出该函数的曲线，以了解它所反映的规律，比如曲线的形状、范围等。这时我们可以用图3所示的添加函数列表命令来实现（注意“图表”菜单只有在你建立了一个新图的时候才会出现，图3所示的新图是用没有数据的空表建立的）。

图3 添加函数图表命令

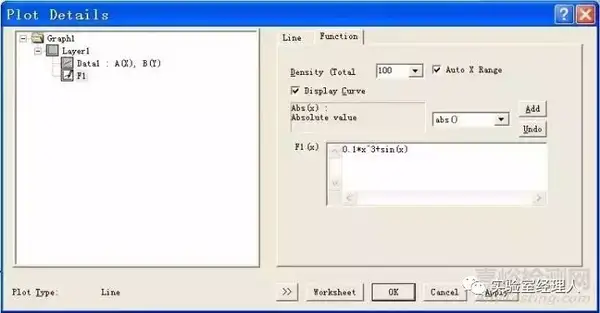
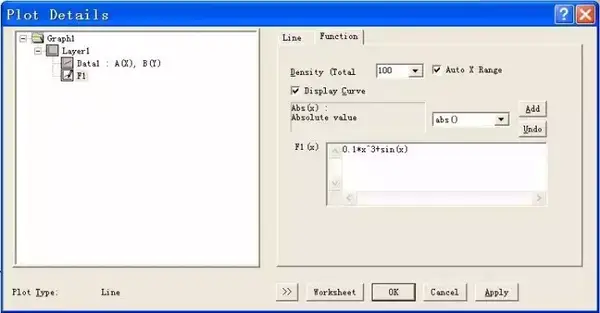
点击“添加函数图表”命令后会弹出图4所示的对话框，输入函数，如0.1*x^3 sin(x)。绘制出的曲线如图5所示。

图4 输入已有函数

图5 绘制出的函数曲线

9. 数据拟合

（1）线性拟合

用实验数据绘出散点图之后，在“分析”菜单中选择“线性拟合”命令即可。

（2）非线性拟合

1）用现有公式拟合

Origin中提供了能够满足绝大多数工程计算的公式。

2）自定义拟合

origin 中虽然提供了强大的拟合曲线库外，但在实际使用中，你可能会发觉在所提供的曲线库中没有你想要拟合的公式。这时你就可以使用用户自定义公式进行拟合。过程如下：

打开主工具栏中analysis（拟合）的non-linear curve fit（非线性拟合）...., 这时会出来一个选择公式界面。
选择编辑公式，需要你提供公式名称以供系统保存；还要提供参数的个数及主变量及因变量符号。
按你需要的公式写在编辑框内，写完后按save进行保存。
现在开始拟合：在action中选dataset，提供主变量和因变量的一些相关参数。
在action中选simulate，在参数中填上你根据数据及其它一些条件确定的粗略的初始参数以及拟合起始点的位置及拟合点数，然后按下create curve就会在图上出现一条拟合曲线，但这往往与期望值差距较大，因此接下来需要进行参数优化。
参数优化采用试错法，根据曲线形状逐渐改变参数，注意，多参数时改变任何一个参数都会改变曲线形状，因此可以一次变一个参数，直到达到满意的形状。
在action中选fit，按下Chi-sqr和10-lit。
在action中选results，按下param worksheet生成拟合曲线及数据。此时可以关闭拟合界面。
在图左上角右键点1，选add/removeplot，将多余的曲线删除，将nlsf系列曲线留下。拟合数据可在param worksheet中看到。

这样就完成了一次自定义曲线拟合。

提示：

R2（拟合优度或确定系数），0≤R≤1，越大表示拟合程度越好

χ2（残差平方和），越小表明拟合程度越好

误差棒用的是标准（偏）差：即真误差平方和的平均数（方差）的平方根，作为在一定条件下衡量测量精度的一种数值指标，也是一系列观测值离散情况的度量。

附：内置函数

abs : 绝对值

acos : x 的反余弦

angle(x,y) : 点(0,0)和点(x,y)的连线与 x 轴之间的夹角

asin : x 的反正弦

atan : x 的反正切

J0 : 零次贝塞耳函数

J1 : 一次贝塞耳函数

Jn(x,n) : n 次贝塞耳函数

beta(z,w): z > 0, w > 0 β函数

cos: x的余弦

cosh : 双曲余弦

erf : 正规误差积分

exp : 指数

ftable(x,m,n) : 自由度为 m,n 的 F 分布

gammaln : γ 函数的自然对数

incbeta(x,a,b) : 不完全的β函数

incf(x,m,n): m,n自由度上限为 x 的不完全 F 分布

incgamma(x,a) : 不完全 γ 函数

int : 被截的整数

inverf : 反误差函数

invf(x,m,n) : m 和 n自由度的反 F 分布

invprob : 正态分布的反概率密度函数

invt(x,n) : 自由度 n 的反 t 分布

ln : x 的自然对数

log : 10为底的 x 对数

mod(x,y) : 当整数 x 被整数 y 除时余数

nint : 到 x 最近的整数

prec(x,p) : x 到 p 的显著性

prob : 正态分布的概率密度

qcd2 : 质量控制 D2 因子

qcd3 : 质量控制 D3 因子

qcd4 : 质量控制 D4 因子

rmod(x,y) : 实数x除以实数y的余数

round(x,p) : x 环绕 p 的准确度

sin : x 的正弦

sinh : x 的双曲正弦

sqrt : x 的平方根

tan : x 的正切

tanh : x 的双曲正切

ttable(x,n) : 自由度为 n 的学生氏t分布

y0 : 第二类型零次贝塞耳函数

y1 : 第二类型一次贝塞耳函数

yn(x,n) : 第二类型 n 次贝塞耳函数

用origin软件处理实验数据（origin数据处理）

相关推荐