主成分分析(PCA)
主成分分析也称主分量分析,旨在利用降维的思想,把多指标转化为少数几个综合指标。在统计学中,主成分分析(principal components analysis,PCA)是一种简化数据集的技术。它是一个线性变换。这个变换把数据变换到一个新的坐标系统中,使得任何数据投影的第一大方差在第一个坐标(称为第一主成分)上,第二大方差在第二个坐标(第二主成分)上,依次类推。主成分分析经常用减少数据集的维数,同时保持数据集的对方差贡献最大的特征。这是通过保留低阶主成分,忽略高阶主成分做到的。这样低阶成分往往能够保留住数据的最重要方面。但是,这也不是一定的,要视具体应用而定。
操作方法
- 01
主成分分析的目的在于降维,使用最少的数据来表示一个样本。让方差大的维度或者说特征来代表样本。

- 02
首先需要对数据进行标准化。 m=mean(data,axis=0) s=std(data,axis=0) data=(data-m)/s
- 03
获得协方差矩阵,用于计算变量间的关系。 获得主要变量及其组合。 c=cov(transpose(data)) eigvalues,eigvectors=linalg.eig(c) indexes=argsort(eigvalues) indexes=indexes[::-1] eigvectors=eigvectors[:,indexes] eigvalues=eigvalues[indexes] eigvectors=eigvectors[:,:k]
- 04
获得处理后的数据,以及计算方差累计值。 x=dot(transpose(eigvectors),transpose(data)) y=(transpose(dot(eigvectors,x))+m)*s print(sum(eigvalues[:k])/sum(eigvalues))
- 05
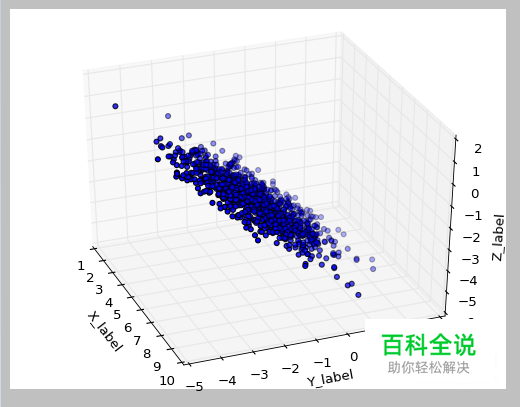
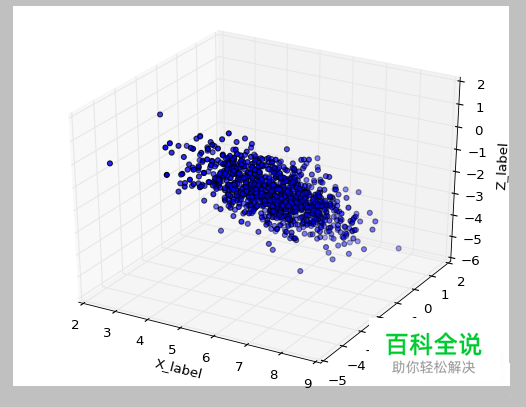
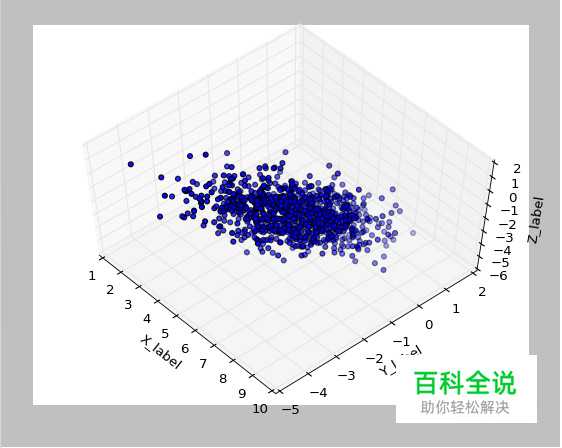
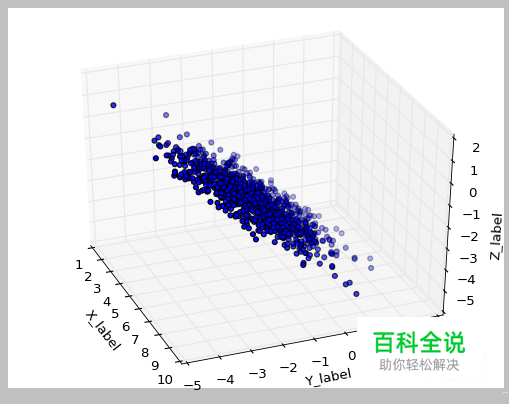
import numpy as np from mpl_toolkits.mplot3d import Axes3D import matplotlib.pyplot as plt from numpy import * x = random.normal(5,.5,1000) y = random.normal(3,1,1000) z=random.normal(0,1,1000) a = x*cos(pi/4) + y*sin(pi/4) b = -x*sin(pi/4) + y*cos(pi/4) c =- z*sin(pi/4) + -y*cos(pi/4) k=1 data=zeros((1000,3)) data[:,0]=a data[:,1]=b data[:,2]=c m=mean(data,axis=0) s=std(data,axis=0) data=(data-m)/s c=cov(transpose(data)) eigvalues,eigvectors=linalg.eig(c) indexes=argsort(eigvalues) indexes=indexes[::-1] eigvectors=eigvectors[:,indexes] eigvalues=eigvalues[indexes] eigvectors=eigvectors[:,:k] print(sum(eigvalues[:k])/sum(eigvalues)) x=dot(transpose(eigvectors),transpose(data)) y=(transpose(dot(eigvectors,x))+m)*s fig=plt.figure() ax=fig.add_subplot(111,projection='3d') ax.scatter(y[:,0],y[:,1],y[:,2],c='b',marker='o') ax.set_xlabel('X_label') ax.set_ylabel('Y_label') ax.set_zlabel('Z_label') plt.show() 代码演示,如上。包括数据生成的方法。

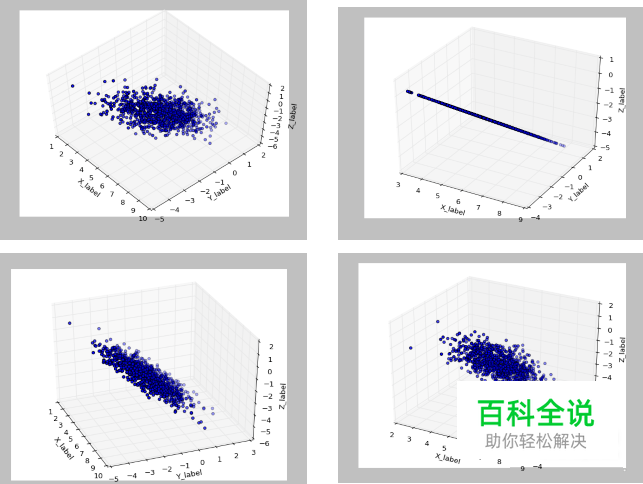
- 06
可以通过改变k值,变换数据,压缩数据。 可视化图形如下。